Preprint (03.05.2006)
Date: Wen, 03 May 2006 18:24:18 GMT
From: redshift0@narod.ru (Alexander Chepick)
Organization:
Newsgroups: sci.physics, alt.sci.physics.new-theories
Subject: Michelson-Morley Experiment
Key words: Michelson-Morley Experiment - the selected reference system

Michelson-Morley Experiment does not testify to Absence of Aether

Alexander M. Chepick Nizhni Novgorod,
e-mail: redshift0@narod.ru

Abstract
There is transformations of coordinates between inertial reference frames in the Absolute space and taking into account results of Michelson-Morley Experiment (MMX).

1. Introduction

On a boundary of 19-20 centuries Michelson and Morley[1] have executed a number of experiments (ллу) on checking of possible influence of a aether's wind on a speed of propagation of electromagnetic waves. Experiment with enough high accuracy has shown, that such influence is absent. Lorentz managed to explain this result at the additional assumption, that Maxwell equations describing distribution of electromagnetic waves, should be identical in all inertial systems of reference (IFR) [2]. The transformations of coordinates obtained by him have named the Lorentz transformations. In the beginning of 20 century Einstein has managed to deduce these transformations from more general theoretical base, named by him the Special Relativity Theory (SRT) [3]. He has called the result of ллу the certificate of absence of an aether.

We shall show that MMX does not demand an absence of aether.

2. The analogy of absolute space

A ship floating on quiet lake, is a source of waves, however speed of these waves does not depend on speed of the ship. Especially, speed of waves cannot depend on the speed of a boat-receiver crossing them. But relative speed of waves depends on speed of movement of water concerning the receiver-observer (only if standards for measurement of speed of waves are not created by this observer with the help of these waves). Also frequency of accepted waves depends on speed of the boat-observer, therefore the observer on the boat can define the speed concerning coast and motionless water of lake - because of distribution of frequencies of accepted waves. (That we on the Earth have managed to execute for a microwave background.) But if the observer does not leave of depth of ocean and moves under water with small speed, he does not receive sound waves from all points of ocean, so he can assume an impossibility of determining of his speed and a constancy of speed of sound in water in any IFR. Thus, independence of speed of light in vacuum from speed of a source or speed of the receiver classically more likely is the certificate of presence of luminiferous environment than its absence.

3. Transformations of coordinates in Absolute space

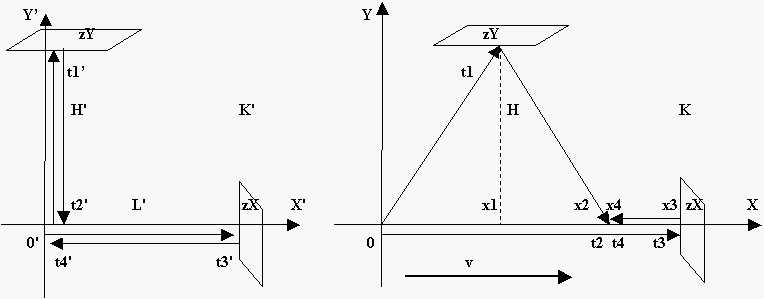
As Maxwell, we shall assume existence of an aether - the isotropic environment in which electromagnetic fluctuations are spreading. We shall show that there is a decision for transformations of coordinates between motionless in aether an IFR K, and moving in aether with absolute speed v an IFR K', and this transformation not contradict to results of ллу. We shall designate on Pic.1 of coordinates of time and a place of movement of a light's signal in IFR K' (on the left) and IFR K (on the right).

Pic.1.
In IFR K' (on the left) the perpendicular rays of light, simultaneously leaving from a point 0', come back into point 0'. In IFR K (on the right) the same rays of light, simultaneously leaving from a point 0, come back in x₄. Results of experiment ллу show that times of return of rays (t₂' and t₄') in K' and (t₂ and t₄) in K coincide with high accuracy..

Let, the beginning of coordinates of IFR K' moves in IFR K with a speed v. We shall write out a general view of linear transformations of coordinates from K into K' in case of concurrence of corresponding axes of coordinates of these IFRs at the initial moment t=0, and axis X is directed in a positive direction of a vector v:

t'=a(v)x+b(v)t;  x'=d(v)x+e(v)t; y'=y; z'=z       (1)

A finding in an obvious kind of functions a(v), b(v), d(v) and e(v) in some conditions, we shall name by the decision of a problem of search of a matrix of transformation of coordinates under these conditions.

As it is known, Einstein has obtained such decision for two IFRs (named Lorentz's transformations[2]:  a(v)=-γv/c², b(v)=d(v)=γ ,  e(v)=-γv,  where  γ=[1-(v/c)²]^-½) under condition of performance in all IFRs of two postulates: speed of light c is a constant, laws of physics are invariant; and assumption that the matrix of transformation depends only on one parameter - of relative speed of IFR. Thus he has refused a hypothesis about existence of an aether, as superfluous, and hypothesis about the selected system of reference, as it is contradicting to the postulates.

Though under such condition Lorentz's Transformation is the unique decision of system (1), nevertheless it does not mean, that under other conditions there will be no other decision of the same system. Within the frames of SRT the any assumption about an aether is impossible as SRT contradicts the main property of a motionless aether - existence of the selected system of reference in which the aether is motionless.

Therefore for aether we must construct another theory - in linear space.

The IFR in which the ether is motionless, is the selected (absolute) system of reference(AFR). Due to isotropic properties of an aether, speed of light in it is isotropic and its value is equal to some constant c in AFR. Therefore synchronization in AFR K can be carried out by Einstein's method or by a method of slow moving clock. But synchronization in IFR K' cannot be carried out on the specified methods as it is not known, whether there will be a light's speed isotropic in K' or a limit of the indication of moved clock will be to exist at aspiring of speed of moving clock to zero. Therefore synchronization in IFR K' can be carried out only by a method of synchronization at which clocks in each IFR are synchronized by simultaneous events in AFR. This method (MSN) does not depend on speed of light, in it coincidence of the moments of time t of two spaced apart (x₁≠x₂) events (t,x₁) and (t,x₂) in AFR corresponds to coincidence of the corresponding moments of time t' of these events (t',x'₁) and (t',x'₂) in IFR (property of a simultaneity of any two events in any IFRs if these events are simultaneous in anyone IFR). These values shall substitute in (1): t'=b(v)t+a(v)x₁; t'=b(v)t+a(v)x₂; and we shall obtain a(v)x₁=a(v)x₂ , that is, a(v)=0. From movement of zero point K' in K with a speed v follows, that e(v)=-d(v)v. Thus, we obtain a system of the equations:

t'=b(v)t;  x'=(x-vt)d(v); y'=y; z'=z       (2)

So, let, AFR K is an absolute system of reference with the cartesian metrics, IFR K' is moving with a speed v in K.

We shall input the designations of various variables in K', involved in the description of experiment ллу (see Pic.1); not shaded coordinates of corresponding events in K are calculated under the formula (2):
t₁' - the moment of reflection of a light's impulse from a mirror z_Y
t₃' - the moment of reflection of a light's impulse from a mirror z_X
t₂' - the moment of return of a perpendicular light's impulse into a point 0'
t₄' - the moment of return of a longitudinal light's impulse into a point 0'
H'  - length of a perpendicular shoulder up to a mirror z_Y
L'  - length of a longitudinal shoulder up to a mirror z_X
x₁' - X-coordinate of a place of reflection of a light's impulse from a mirror z_Y
x₃' - X-coordinate of a place of reflection of a light's impulse from a mirror z_X
x₂' - coordinate of a place of return of a perpendicular light's impulse
x₄' - X-coordinate of a place of return of a longitudinal light's impulse
Я₀₁ - speed of moving of a light's impulse to a mirror z_Y in K'
Я₁₂ - speed of moving of a light's impulse from a mirror z_Y in K'
Я₀₃ - speed of moving of a light's impulse to a mirror z_X in K'
Я₃₄ - the module of speed of moving of a light's impulse from a mirror z_X in K'
 H  - length in K of a perpendicular shoulder up to a mirror z_Y
 L  - length of the moving longitudinal shoulder, measured in IFR K

Write down the equation of the link for all variables:

In K' :
x₂' = x₄' = 0           (3) - beams return into zero point,
H' = Я₀₁t₁'            (4) - hit of the beam in a mirror z_Y,
H' = Я₁₂(t₂'-t₁')     (5) - return of a beam from a mirror z_Y,
L' = x₃' = Я₀₃t₃'     (6) - hit of a beam in a mirror z_X,
L' = Я₃₄(t₄'-t₃')      (7) - return of a beam from a mirror z_X.

Let's especially note parity L' =H'  (8) (it follows of, what the observers in K' (in particular - we) are obliged to operate with the same standard of length, irrespective of a direction of this standard); and also parities H=H'   (9) and H=L' =d(v)L   (10), obtained from (2) and from condition of a simultaneity of measurement in K of length L of moving shoulder L'.

In K :
x₁ = vt₁                            (11) - a way of the point 0' during time t₁,
(x₂-x₁) = v(t₂-t₁)               (12)  - a way of the point 0' during time t₂-t₁,
H² + x₁² = Я²t₁²                (13) - length of a way of a beam to a mirror z_Y,
H² + (x₂-x₁)²= Я²(t₂-t₁)²   (14) - length of a way of a beam from a mirror z_Y,
vt₃+L = x₃ = Яt₃                (15) - a way of beam during time t₃,
vt₄ = x₄ =x₃ - Я(t₄-t₃)         (16) - a way of beam during time t₄-t₃,

Zero result of ллу (a picture of an interference does not change during turn of the device [4, Р.3, with 27]) shows that to the interference's screen both signals come simultaneously in identical phase. They go along the same way in the same conditions from a prism to the screen, so they radiate from the prism also at the same moment and at single-phase, and this phase does not depend on a corner of turn of the device. It is possible, only if in K' impulses of light come in a point 0' simultaneously. Hence, from ллу follows, both signals in K' come back to a point 0' (practically) simultaneously, that is: t₄' ≈ t₂'   (17).

From (11-14) follows: 2x₁=x₂  (18), t₂ =2t₁   (19),   t₁ =γм/Я  (20)
From (15) follows: t₃ =x₃/Я = L/(c-v)  (21)
From (16,22) follows: t₄ =x₄/v = 2x₃/(c+v)= 2γ²L/Я  (22)
Fron a construction of IFR K' follows: x₁' =x₂' =x₄' =0  (23) , as that are coordinates of begin of frame  K'. 
Hence from (2,19,20) follows: t₁' =b(v)t₁ =b(v) γм/Я   (24), t₂' =2b(v) γм/Я    (25)
From (2,21,22) follows: t₃' =b(v)t₃ =b(v)L/(c-v)  (26), t₄' =2b(v)γ²L/Я   (27)
From (17,25,27) follows: м ≈ γL   (28)

We assume that a relation t₄' ≈ t₂'  is an experimental manifestation of precise equality t₄' = t₂'  (29), and we obtain from (10,28) a value of a function  d(v): d(v)=γ  (30).

Considering the device (interferometer of Michelson) as the light's clock making one full cycle of actions from the beginning of movement of a light's impulse up to his return to the same point; and supposing "one full cycle of the device" as a time unit in any IFR, we obtain at the analysis of movement of an impulse of light along a shoulder H' that from the point of view of IFR K one full cycle t₂' of clock in IFR K' will be executed during time  γt₂ by the same device motionless in K, by virtue of movement in K a light's impulse with identical speed on a hypotenuse and on a cathetus accordingly (see Fig.1). That is, time in terms of "a full cycle" in K' goes more slowly in  γ times, than in terms of "a full cycle" in K. But this particular case of comparison of time in different IFRs should be expressed by the general formula (2). Whence in view of the formula t'=b(v)t follows:  b(v)=1/γ   (31).

We shall calculate speeds of movement of impulses of light in IFR K' :
From (4,5,8,24,25,31) follows: Я₀₁ =Я₁₂ =H'/t₁'=c/(b(v)γ)=c        (32)
From (6,10,27,30,31) follows: Я₀₃=L'/t₃' =γ(c-v)/ b(v)=c/(1+v/c)   (33)
From (7,10,26,27,30,31) follows: Я₃₄= L'/(t₄'-t₃')= c/(1-v/c)          (34)

Hence, in K' we receive anisotropic speed of light. Having designated in K'   a' - a corner of a deviation of speed of light from a direction of speed v, we shall receive the general formula of speed of light in K' :

Я'(v,a')=c/(1+(v/c)cos a')      (35)

4. Conclusions

1. Michelson-Morley experiment does not deny an ether and the selected system of reference.

2. There is a transformation of coordinates in the absolute space from AFR into IFR not contradicting to results of Michelson-Morley experiment:
  t'=t/γ; x'=γ(x-Vt); y'=y; z'=z.

References:
[1] Miller D.C Significance of the ether-drift experiments of 1925 at Mount Wilson. Sd. 1926. Vol. 68, N 1635.
[2] Lorentz H.A.The theory of electrons and its application for the phenomena of light. (Rus) (M.: Gos. izdat. tehn.-theor. Lit., 1953, p. 280-307)
[3] Einstein A. To electrodynamics of moving bodies. (Rus) Assembly of works, v.1. M., Nauka, 1965.
[4] The Phisical Encyclopedia, (Rus) (M., Sovetskaya Encyclopedia,1990, v.3,p.27)

- - - - - - - -
Top       Rus                     Eng

Last correction 08.03.2008 21:02:15