Preprint (16.06.2009)
Date: Tue,16 Jul 2009 10:08:18 GMT
From:redshift0@narod.ru (Alexander Chepick)
Organization:
Newsgroups: sci.physics, sci.astro, alt.sci.physics.new-theories
Subject: СЭТ - скорость света в среде
Key words: Абсолют - СЭТ - теория стационарного эфира - анизотропия -
Абсолютное преобразование - Мандельштам - Игл - Тангерлини -
скорость света в среде.
PACS: 01.55.+b, 01.65.+g, 98.80
Формула скорости света в среде для инерциальной системы координат в теории СЭТ
А.М.Чепик, Нижний Новгород,
e-mail: redshift0@narod.ru
Абстракт
В статье ставится и решается задача вывода формулы скорости света в среде с известным показателем преломления в рамках теории стационарного эфира (СЭТ) на основе классического закона преломления. Принятая в классической оптике и СТО ортогональность светового луча в среде и его фронта волны оказывается нарушенной в СЭТ, где угол между лучом и фронтом волны зависит от скорости света в заданном направлении.
1. Введение
В этой статье ставится задача демонстрации (в рамках теории стационарного эфира (СЭТ)[1]), вывода формулы скорости света в среде, неподвижной относительно наблюдателя, на основе выполнения классического закона преломления.
Показатель (абсолютный) n преломления линейной среды определяется через связь угла падения "i" светового луча, идущего в вакууме, и угла преломления "r" в среде, отсчитываемых от перпендикуляра к поверхности раздела сред в точке преломления луча, причём этот перпендикуляр находится в одной плоскости с падающим и преломлённым лучами (закон Снелля [2,т.4,с.106-107, В.И.Малышев]):
n = sin i /sin r . (1)
В линейной оптике считается, что величина n характеризует среду в целом, тем не менее, n зависит от частоты света (длины волны), его поляризации и интенсивности, температуры среды, внешнего давления, даже от угла падения света, и связана с электромагнитной проницаемостью среды. Также известно, что если среда изотропна и скорость света не зависит от направления в пространстве, то в этом случае показатель n преломления света равен отношению скорости света "c" в вакууме к скорости света "cn" в среде [2,т.4,с.107, В.И.Малышев]:
n = sin i /sin r = c/cn . (2)
Естественно, что этот закон выведен для фазовой скорости света.
В других теориях закон (2) не обязан выполняться, и необходимо различать показатель преломления n = sin i /sin r и показатель отношения скоростей света в двух средах nc = c/cn.
В теории стационарного эфира, где
скорость света c(θ) в инерциальной
системе координат (ИСК) с
ортогональными осями X,Y,Z в вакууме
зависит от направления θ
относительно вектора V скорости
ИСК в Абсолютной системе координат (АСК),
известно, что в среде скорость света
также зависит от скорости V и от
угла θ. В СЭТ необходимо различать
не просто показатель преломления n для вакуума
и среды, и показатель отношения скоростей света в
этих же двух средах nc, но и
учитывать скорость движения среды, и скорость движения наблюдателя.
Для однозначного понимания предлагаю обозначать:
n - показатель в АСК преломления света в
неподвижной в АСК среде;
n(W) - показатель преломления света в АСК в среде,
движущейся в АСК со скоростью W;
n' - показатель преломления света в ИСК в среде,
неподвижной в ИСК, которая движется в АСК со скоростью V;
n'(W) - показатель преломления света в ИСК в среде,
движущейся в АСК со скоростью W, если ИСК движется
в АСК со скоростью V;
и для тех же направлений света в вакууме и среде:
nc - показатель в АСК отношения скоростей
света в вакууме и в неподвижной в АСК среде;
nc(W) - показатель в АСК отношения скоростей
света в вакууме и в среде, движущейся в АСК со скоростью W;
n'c - показатель в ИСК отношения скоростей
света в вакууме и в среде, неподвижной в ИСК,
которая движется в АСК со скоростью V;
n'c(W) - показатель в ИСК отношения скоростей
света в вакууме и в среде, движущейся в АСК со скоростью W,
если ИСК движется в АСК со скоростью V.
Формулы этих величин и соотношения между ними предстоит еще вывести.
Не исключено, что величина n' окажется зависящей от V и от θ, хотя в настоящее время эта зависимость пока экспериментально не обнаружена [3],[4]. Эффект Френеля положительно решает вопрос зависимости n'c(W) от относительной скорости среды, движущейся в ИСК (причём именно показателя отношения скоростей, а не показателя преломления). Однако в этой статье решается вопрос о скорости света в среде, неподвижной в ИСК, поэтому даже если показатель преломления среды в ИСК зависит от V и θ, то эта зависимость не проявится, поскольку не имеет значения, по какой причине n'c имеет конкретную величину в заданном направлении в среде - из-за свойств среды или из-за движения среды в эфире.
Анизотропия скорости света в ИСК является следствием преобразований координат между АСК и ИСК. Вывод этих преобразований, например, показан в статье [5,§5] :
A(V): t'=t/γ; x'=γ(x-Vt); y'=y; z'=z , (3)
где (t,x,y,z) - координаты события в АСК, (t',x',y',z')
- координаты того же события в ИСК,
скорость V ИСК в АСК
параллельна оси X, γ-1=![]() .
.
Вывод этого преобразования получен из постулатов о существовании выделенной системы координат, неподвижной в эфире; из нулевого результата эксперимента Майкельсона-Морли, а также из метода натуральной синхронизации [5,§3].
Первым (согласно Г.Б. Малыкину [6]) предложил рассматривать это преобразование Ф.Р. Тангерлини [7] в 1958 году, однако сам Тангерлини в более поздних комментариях [8] к своей диссертации [7] пишет о ставшей ему известной статье А. Игла (Albert Eagle)[9] 1938 года (и в честь которого это преобразование следовало бы называть Преобразованием Игла), в которой Игл приводит указанные преобразования (3), но с аргументацией, направленной против Специальной теории относительности. Затем это преобразование придумал Ш. Маринов [10], затем Р. ДеВитт [11]. В России первым о нахождении таких преобразований заявил Н.В. Купряев [12], который на данный момент является крупнейшим специалистом в этой области, затем Обухов и Захарченко [13], затем автор этой статьи[14]. Все они изобретали это преобразование независимо друг от друга, так как до начала 21 века статьи по теории СЭТ достаточно широкого распространения не находили. Сам Тангерлини назвал преобразование (3) Абсолютным преобразованием Лоренца (Absolute Lorentz transformation [7]), однако такое название не привилось.
Я предлагаю называть преобразование (3) - Абсолютное преобразование, поскольку все авторы, открывшие его, связывали его с Абсолютной системой координат, и, как оказалось, оно в виде (3) связано только с Абсолютной системой координат, и не описывает преобразование координат ни из какой другой системы.
Справка:
Следует отметить, что Л.И.
Мандельштам (1934 г.)[15],[6],
Л.Д. Ландау и Е.М.Лифшиц (1967г.)[16],
Л.А. Логунов (1987 г.)[17] знали о
возможности представления времени в ИСК в
виде t'=t/γ; однако не сформулировали
вывод о возможности существования
преобразований (3) координат из абсолютной
системы отсчета. В частности, Логунов
описал так называемое "координатное
время": "2.Поворот оси t без
изменения ориентации оси х описывается
преобразованием Х = х; T=t + wx/c2 (16.3)"[17,с.118].
Умножив Преобразование Лоренца на это преобразование,
можно получить Абсолютное преобразование (3), однако
без постулата о существовании абсолютной
системы координат оно оказалось Логунову
не нужным.
Формула скорости света в среде в рамках СЭТ разными методами получена Тангерлини [12,ф.(5.5)], Обуховым и Захарченко [13,ф.(36)], однако эти методы дают одну и ту же формулу в случаях анизотропного и изотропного показателя преломления в ИСК.
В этой статье будет выведена формула зависимости угла между лучом света и фронтом его волны от направления света в ИСК, выведено дифференциальное уравнение для зависимости скорости света от направления распространения света в ИСК в среде, а затем найдено решение этого уравнения для изотропного показателя преломления и указан метод решения для анизотропного показателя преломления в ИСК.
2. Расчет угла между фронтом волны и вектором скорости света в среде ИСК СЭТ
Согласно закону Снелля, падающий и преломленный лучи, а также перпендикуляр, построенный к поверхности раздела сред в точке падения луча, находятся в одной плоскости, которую обозначим P0. Заметим, что с помощью поворота базиса ИСК вокруг оси OX можно добиться того, что P0 будет перпендикулярна координатной плоскости PXOZ . Именно в таком базисе будем решать вопрос в плоскости P0 о скорости света в среде. Для этого рассмотрим фронт волны в плоскости P0. Если скорость света в среде анизотропна, то фронт волны от центрального источника в разных направлениях будет через время t находиться на разных расстояниях, то есть, не будет сферическим.
Вычислим в среде, неподвижной в ИСК, угол µ в плоскости P0 между лучом света от неподвижного центрального монохромного источника и линией фронта световой волны, находящейся в плоскости P0 в положительном направлении от рассматриваемого луча. Назовём для краткости этот угол - угол фронта волны. Отметим, что угол θ анизотропии ИСК измеряется от положительного направления оси X, а остальные углы измеряются от любого заданного направления, при этом положительным будет угол, измеряемый против часовой стрелки.
Обозначим cn(θ) - модуль вектора скорости света в ИСК в среде. Пусть в ИСК имеется некий окруженный эфиром неподвижный достаточно объёмный многогранник, состоящий из вещества (среды) с показателем преломления n, определяемым по закону Снелля (1). Пусть внутри многогранника в точке O имеется монохромный точечный источник света. Внутри многогранника построим фигуру G, образованную точками, в которые попадают лучи света от этого источника спустя время t после излучения.
Рассмотрим конкретный луч, направленный из точки O под углом θ к оси OX, который за время t попал в точку A(x,y,z). Построим линию OU - ортогональную проекцию этого луча AO на координатную плоскость PXOZ . Плоскость, содержащую вектора OU и OA, обозначим P0, по построению она ортогональна PXOZ . P0 представлена плоскостью листа на Рис.1. Линия OU будет являться осью координат в плоскости P0 . Направление луча AO (угол θ ) в этом случае однозначно выражается через его проекции: угол ψ отклонения оси OU от оси OX (см. Рис.1) в плоскости PXOZ , отсчитываемый от оси OX, и угол ε в плоскости P0 , отсчитываемый от вектора OU :
cos θ=cos ψ cos ε . (4)
Граница фигуры G в плоскости P0 образует некоторую кривую, проходящую через точку A(x,y,z). В этой плоскости необходимо найти угол µ фронта волны для рассматриваемого луча AO, а затем найти связь между cn(θ), θ и n (или c'n(θ), θ' и n' для ИСК, однако далее в целях упрощения обозначений мы не будем использовать "штрихи" в смысле принадлежности величин к ИСК, поскольку ясно, что в этой главе речь идёт о произвольной системе координат, а в следующих главах рассматривается только ИСК). В случае, когда среда - это эфир (n=n'=1), такая связь в ИСК известна [1]:
c1(θ)=c/(1+ β·cos θ) . (5)
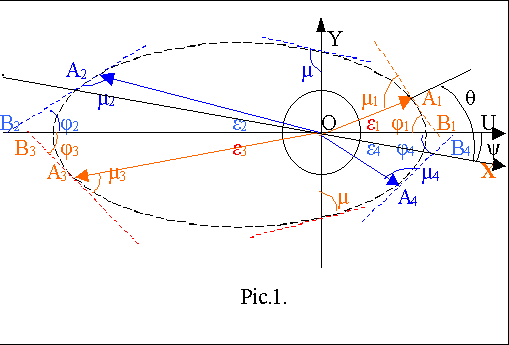
Рис.1: Множество точек A (фронт волны) для всех направлений θ, куда попали лучи света за время t, показано в виде эллипса в плоскости P0, проходящей через ось OY и ось OU, ось OU повёрнута относительно оси OX на угол ψ, угол UOA обозначим ε, эти углы связаны с углом θ соотношением: cos θ= cos ψ cos ε. Для функции c1(θ) показаны варианты углов µ между лучом света и фронтом световой волны в плоскости P0 при различных направлениях φ касательной к фронту волны. Приведенные рассуждения применимы и в изотропной, и в анизотропной среде.
Для расчета угла фронта волны используем свойство производной y'(x)x любой функции y(x): y'(x)x = dy(x)/dx = tg(φ), где φ - угол отклонения (от оси X) касательной к графику функции y(x) в точке A(x,y). Зная угол φ, легко вычислить угол фронта волны для вектора скорости света.
Поскольку искомая функция cn(θ) в общем случае зависит от двух переменных ψ и ε, то угол наклона касательной к функции cn(ψ,ε) будет определяться частными производными по ψ и ε. Будем искать решение cn(ψ,ε) в множестве гладких непрерывных функций, следовательно, имеющих непрерывные производные по ψ и ε. Но в плоскости P0 угол ψ постоянен, следовательно, для функции cn(ψ,ε) в этой плоскости частная производная по ε является полной производной c'n(ψ,ε) =dcn(ψ,ε)/dε.
В ИСК свет в неподвижной среде может распространяться в любых направлениях, следовательно, cn(ψ,ε)>0. Обозначим:
fn = c'n(ψ,ε)/cn(ψ,ε). (6)
На Рис.1 видно, что угол µ (0≤ µ< π) в плоскости P0 является внешним или внутренним в треугольниках ОAKBK, в зависимости от ситуации с углом наклона касательной (варианты ситуаций показаны в разных квадрантах K). Угол µ выражается через углы εK и φK, угол εK в этом треугольнике выражается через угол ε радиус-вектора, угол φK выражается через угол φ наклона касательной:
| Угол \ вариант | I | II | III | IV |
| εK | ε | π - ε | ε - π | 2π - ε |
| φK | π - φ | φ | 2π - φ | φ - π |
| µK | π + ε - φ | ε - φ | π + ε - φ | ε - φ |
Выпишем координаты точки A(x,u) в
плоскости P0 :
u= u(ε)= tcn(ψ,ε) cos ε, y= y(ε)=
tcn(ψ,ε) sin ε.
Выразим tg φ через fn и ε: tg φ = dy/du= [dy(ε)/dε]/[du(ε)/dε]=
=[t(c'n(ψ,ε) sin ε + cn(ψ,ε) cos ε)]/[t(c'n(ψ,ε) cos ε - cn(ψ,ε) sin ε)]=
=[fn sin ε + cos ε]/[fn cos ε - sin ε].
Поскольку ctg µ не зависит от рассмотренных ситуаций, то оказалось возможным выразить ctg µ через fn:
ctg µ = cos(π + ε - φ)/sin(π + ε - φ)= cos(ε - φ)/sin(ε - φ)=
= [cos ε+ tg φ sin ε]/[ sin ε- tg φ cos ε]= - fn .
Таким образом:
ctg µ= - fn . (7)
Отсюда получаем: sin µ=1/(1+ fn2)1/2; cos µ= - fn/(1+ fn2)1/2.
В случае, если cos φ=0, то аналогичные вычисления проведем через ctg(φ)= du/dy , и увидим, что этот случай учтен в формуле (7).
Для угла µ', дополнительного к углу µ: µ'= π -µ, получаем:
sin µ'=1/(1+ fn2)1/2; cos µ'= fn/(1+ fn2)1/2 , ctg µ'= fn . (8)
Таким образом, в СЭТ угол µ между лучом света и его фронтом волны не обязательно образует прямой угол. Однако, если в среде окажется, что cn(θ) постоянна, то для такой функции будет fn=0 и µ=±π/2.
3. Угол фронта волны, идущей в эфире от центрального источника
Рассчитаем в ИСК по ф.(5) в плоскости P0 угол µ1 фронта волны, идущей в эфире (n=1) от центрального источника:
f1 =[dc1(ψ,ε)/dε]/ c1(ψ,ε) = β·cos ψ·sin ε/(1+ β·cos ψ·cos ε) . (9)
И по формуле (7) получаем, что в эфире будет:
cos µ1 = - β·cos ψ·sin
ε/ ( 1+ 2β·cos ψ·cos ε
+ β2·cos2ψ)1/2
sin µ1 = (1+ β·cos ψ·cos ε)/
( 1+ 2β·cos ψ·cos ε + β
2·cos2ψ)1/2
(10)
ctg µ1 = - β·cos ψ·sin ε/(1+
β·cos ψ·cos ε)
А для дополнительного угла µ'1 по формуле (8) будет:
cos µ'1 = β·cos ψ·sin
ε/ ( 1+ 2β·cos ψ·cos ε +
β2·cos2ψ)1/2
sin µ'1 = (1+ β·cos ψ·cos
ε)/
( 1+ 2β·cos ψ·cos ε + β
2·cos2ψ)1/2
(11)
ctg µ'1 = β·cos ψ·sin ε/(1+
β·cos ψ·cos ε)
4. Уравнение движения фронта волны в среде
Предыдущие рассуждения касаются углов, следовательно, от точки начала координат не зависят, это позволяет далее началом координат считать точку падения луча света на поверхность раздела сред.
Пусть в ИСК заданы плоскость раздела вакуума и среды, углы падения и преломления. Рассчитаем в ИСК угол µn фронта волны от центрального источника, идущей в среде.
Рассмотрим луч AO, падающий на поверхность POCD раздела сред в точке O, преломляющийся, и идущий далее в среде. По условию выполняется закон Снелля (1): падающий луч AO, преломлённый луч OB и перпендикуляр GOH к поверхности POCD находятся в одной и той же плоскости P0 (представленной плоскостью листа на Рис.2). Плоскости P0 и POCD ортогональны и пересекаются по линии CD. Очевидно, что ось OY лежит в плоскости P0.
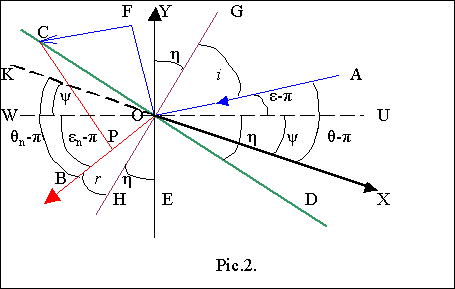
Рис.2: Луч AO падает на поверхность раздела сред, луч OB преломляется в среде. Линия WU - это проекция падающего луча AO на плоскость XOZ. Также линия WU - это проекция оси OX на плоскость P0, линия KOX лежит вне плоскости P0, если угол ψ=∠XOU≠0.
В плоскости P0 : GH - перпендикуляр к CD в точке O, обозначим угол наклона CD к линии WU: ∠DOU= η, измеряя его от линии раздела сред, тогда: -η = ∠UOD = ∠YOG= ∠WOC, +η = ∠DOU =∠GOY=∠COW=∠HOE. Обозначим i - угол между падающим лучом AO и перпендикуляром GH, при этом луч направлен под углом ε= π+∠UOA к оси U, BO - преломлённый луч под углом r к перпендикуляру GH, при этом луч направлен под углом εn= π+∠WOB к оси U, FC - луч света, параллельный AO (луч света считаем достаточно тонким), FO - линия фронта волны в эфире, СP - тот же фронт волны спустя время T, но уже в веществе. Углы ∠ AOF и ∠ OPC - дополнительные к µ1 и к µn , потому далее для вычисления µ'1 и µ'n воспользуемся формулой (8).
Выразим в плоскости P0 угол ε :
ε= π+∠ UOA=π+∠ UOY- ∠ GOY - ∠ AOG= 3π/2-η-i (12)
Отметим дополнительный угол фронта волны µ'1 в треугольнике COF :
∠ CFO = ∠ AOF = µ'1 ,
∠ YOF =∠ AOF - ∠ GOY -∠ AOG = µ'1-η- i ,
∠ FOС= ∠ YOW - ∠ COW - ∠ YOF = π/2 -η - (µ'1-η- i)= π/2+ i - µ'1 .
Пусть фронт волны проходит отрезок FC за время T>0 , тогда из теоремы синусов для треугольника COF можно выразить отрезок CO>0 (на Рис.2): sin(∠CFO)/CO=sin(∠ FOС)/FC, т.е.:
sin µ'1 / CO = cos(µ'1- i) / (Tc1(θ)) . (13)
CP - фронт волны в среде, ∠ OPС = µ'n - дополнительный к µn .
∠ COP = ∠ COH - ∠ BOH= π/2 -r .
∠ PСO = π - ∠ COP- ∠ OPС= π/2 +r - µ'n .
Направление εn вектора скорости света в среде в плоскости P0 будет
εn =ε + i - r= 3π/2 - η - r (14)
За то же время T>0 в среде фронт волны пройдет меньшее расстояние OP=Tcn(θn). Тогда из теоремы синусов для треугольника COP можно выразить тот же отрезок CO: sin(∠ PСO)/OP = sin(∠ OPC)/CO, т.е.:
cos(µ'n-r) / (Tcn(θn)) = sin µ'n / CO . (15)
Из уравнений (13) и (15) следует основное уравнение связи скоростей волны:
cos(µ'n-r) / ( sin (µ'n) cn(θn)) = cos(µ'1- i) / ( sin(µ'1) c1(θ)). (16)
Очевидно, что при n=1 получается тождество, так как никакого преломления не будет: r=i, θn = θ, cn(θn) = c1(θ), µ'n = µ'1.
Далее считаем, что n>1.
5. Дифференциальное уравнение движения фронта волны в среде
Раскроем косинусы в ф.(16):
(ctg µ'n cos r + sin r) /cn(θn) = (ctg µ'1 cos i + sin i) /c1 (θ). (17)
Для дополнительных углов имеем ctg µ'n=fn , ctg µ'1=f1 , поэтому из ф.(17) получаем:
(fn cos r + sin r) / cn(θn) = (f1 cos i + sin i) / c1( θ). (18)
Учитывая, что в плоскости P0 угол θn выражается через ψ и εn , а угол θ - через ψ и ε, и по формуле (6): fn = c'n(ψ,εn)/c n(ψ,εn), формулу (18) можно записать в виде :
(cos r) c'n(ψ,ε n)/cn2(ψ,εn) + (sin r) /cn(ψ,εn) =
= (cos i) c'1(ψ ,ε)/c12(ψ,ε) + (sin i) /c1(ψ,ε) (19)
Учтём соотношения для углов i= 3π/2 - η - ε и r = 3π/2 - η - εn , которые показывают, что при неподвижной установке, то есть, при постоянном угле η, угол i зависит от угла ε, а угол r зависит от угла εn .
Таким образом, cos r = - sin(η+εn), sin r = - cos(η+εn), и левая часть ф.(19) равна:
- sin(η+εn) c'n(ψ ,εn) / cn2(ψ,εn) - cos(η+εn)/cn(ψ ,εn).
Обратим внимание, что условие sin(η+εn)=0 означает, что преломлённый угол параллелен плоскости раздела сред, чего при n>1 не может быть, следовательно, sin(η+εn)≠0.
Сделав замену переменных g(εn)= sin(η+εn)/cn(ψ ,εn), и взяв её производную g'(εn) по εn , получаем, что левая часть ф.(19) равна :
g'(εn)-2 ctg(η +εn)g(εn) .
В правой части уравнения (19) все величины известны. Здесь имеем:
cos i = - sin(η+ε), sin i = - cos(η+ε), , sin i =n sin r
c'1(ψ,ε)/c12(ψ,ε)= (β/c)·cos ψ·sin ε .
Преобразуем правую часть ф.(19) в соответствии с ф. (5) и ф.(11), и получаем:
(cos i) c'1(ψ,ε)/c12(ψ,ε)+ (sin i) /c1(ψ,ε) = (-1/c) (β cos ψ cos η +n cos(η+ε n)).
Таким образом уравнение (19) является линейным дифференциальным уравнением первого порядка:
g'(εn) -2 ctg(η+ εn)g(εn) = (-1/c) (β cos ψ cos η +n cos(η+εn)) (20)
6. Решение уравнения движения фронта волны
Известно, что линейное дифференциальное уравнение (20) первого порядка имеет решение вида
g(εn) =m(εn) {(-1/c) ∫ [(β cos ψ cos η + n cos(η+εn))/ m(ε n) ]dεn-C} (21)
где m(εn) =exp[2 ∫
ctg((η+εn)dεn]
=sin2(η+εn),
C -
произвольная величина, не зависящая от εn
(см.[18,с.269, ф.(9.2-15)]). Напомним
также, что β, ψ, η не зависят
от εn .
Интеграл в g(εn) в ф.(21) легко вычисляется для показателя преломления n, не зависящего от εn . Для таких n получаем:
cn(ψ,εn) = sin(η+εn) /g(εn) =c/[β cos ψ cos η cos(η+εn) + n +C sin(η+εn)]
Если записать C= β cos ψ sin η +D, где D - другая произвольная величина, не зависящая от εn , то получим обобщенное решение уравнения (19) в виде:
cn(ψ,εn) = c /[n + β cos ψ cos εn + D sin(η+εn)]. (22)
В качестве краевого условия для получения частного решения уравнения (22) возьмём соображение, что скорость света в среде в заданном направлении не может зависеть от того, какой был наклон η границы сред при входе луча в среду, так как эта скорость должна быть равна скорости света в этом направлении от источника внутри среды. В ф.(22) величины cn(ψ,εn), ψ, c, n, β, εn, от η не зависят. Значит, от η не зависит и D·sin(η+εn), обозначим эту величину z и выпишем все условия вместе, то есть:
D·sin(η+εn) = z -
не зависит от η ;
(23)
где εn не зависит от η,
D не зависит от εn.
Таким образом, для любой заданной величины εn величина z должна быть постоянной для всех значений η, но в точках η = -εn +kπ будет z=0. Следовательно, z=D·sin(η+εn)=0 для любых εn и для любого η, отсюда D=0.
С учётом ф.(4), для n, не зависящего от εn , из ф. (22) получаем формулу:
cn(θn) = c /[n + β cos θn] (24)
И поскольку поворот системы координат вокруг оси X, сделанный для удобства расчёта, не влияет на величину угла θn, то эта формула верна и в первоначальной системе координат ИСК.
Для показателя преломления n, зависящего от направления распространения света при фиксированном положении тела в ИСК, формула скорости будет иной, вычисляемой с помощью уравнения (21). Отметим, что метод Тангерлини [7,ф.(5.5)] и метод Обухова и Захарченко [13,ф.(36)] дают для скорости света в среде формулу, в знаменателе которой стоит именно показатель преломления n для АСК, а формула (24) содержит показатель преломления n' и угол θ'n в ИСК. Таким образом, формула в [7,ф.(5.5)] внешне похожа на формулу (24), но имеет другой смысл, поскольку не доказано, что что в АСК и ИСК одна и та же неподвижная среда имеет одинаковые показатели преломления n=n'. К тому же, сама формула (24) является лишь частным случаем формулы (21).
7. Выводы
1. Привычная в классической оптике и СТО ортогональность светового луча и его фронта волны в среде оказывается нарушенной в СЭТ, где угол между лучом и фронтом волны зависит от скорости света в заданном направлении.
2. В статье в рамках теории стационарного эфира (СЭТ) выведена формула скорости света в среде с известным показателем преломления.
3. В отличие от применяемых ранее методов, полученное в статье дифференциальное уравнение (21) позволяет в явном виде вычислить формулу скорости света в среде также и в случае зависимости показателя преломления n от направления распространения света. Причём именно более сложная формула, чем (24), может помочь найти объяснение, почему максимумы разностей времени прохождения света в прямом и обратном направлении не происходят в моменты, когда максимальна проекция пути движения света на вектор скорости Земли в системе координат микроволнового фонового излучения (в которой, предположительно, эфир неподвижен).
4. Таким образом, скорость света в среде зависит от направления луча. Частным случаем из этого вывода получается эффект ДеВитта [11] и эффект Кахилла[19].
И вообще, почему бы физикам-экспериментаторам не повторить измерения Кахилла или ДеВитта, фиксируя (с помощью двух несинхронизированных атомных часов) разность времени прохождения света в прямом и обратном направлении в вакууме или в веществе, и не убедиться в переменности скорости света в течение звездных суток?
Особая благодарность - Н.В. Купряеву (Самарский филиал ФИАН).
Литература:
1. Н.В. Купряев
"Электродинамика с позиции
стационарного эфира", Изв.Вузов, Физика
№8, 63 (2001)); и Н.В. Купряев "Анализ
расширенного представления
преобразований Лоренца", Доклады
независимых авторов, Вып.3, 129 ("DNA",
Россия-Израиль (2006)).
2.Физическая энциклопедия, (М.,
СЭ/БРЭ, 1988-1998.)
3. Н.В. Кравцов, В. В. Рагульский,
Квантовая электроника 30,1025 (2000).
4. В.В. Рагульский, Изв. АН.
Серия физическая 63, 818 (1999).
5. А.М. Чепик "Абсолют.
Основные принципы", ж. "Актуальные
проблемы статистической радиофизики",
2007, т.6, с.111-134
( http://www.mptalam.org/a200709.html
, http://www.mptalam.org/200709.pdf
) (
http://redshift0.narod.ru/Rus/Stationary/Absolute/Absolute_Principles_3_3.htm)
6. Малыкин Г.Б.,
Паралоренцевские преобразования, УФН, т.179,
№ 3 (Март 2009 г.) http://ufn.ru/ufn09/ufn09_3/Russian/r093e.pdf
7. Tangherlini F.R. "The velocity of light in
uniformly moving frame",
PhD Thesis (Stanford: Stanford Univ., 1958) and Tangherlini F.R. Suppl.
Nuovo Cimento 20 1 (1961)
8. Tangherlini F.R. "Preface of 2009 to "The
Velocity of Light in Uniformly Moving Frame" ", The Abraham
Zelmanov Journal - Vol. 2, 2009
9. Eagle A. Phil. Mag., 1938, vol. 26, 410; Phil. Mag.,
1939, vol. 28, 592; Phil. Mag., 1939, vol. 28, 694.
10. Marinov S. Eppur si muove (East-West, Graz, 1987,
англ. яз.), first ed. 1977 (
http://www.ptep-online.com/index_files/books_files/marinov1987.pdf)
11. R. De Witte, Website
http://www.teslaphysics.com/DeWitte/general.htm
R.Cahill, The Roland De Witte 1991 Experiment (to the Memory of Roland De Witte), http://www.ptep-online.com/index_files/2006/PP-06-11.PDF
12. Н.В. Купряев "Расширенное
представление преобразований Лоренца", Изв. вузов. Физика №7, 8 (1999)
13. Обухов Ю.А.,Захарченко И.И.
Светоносный эфир и нарушение принципа
относительности. Физическая мысль России,
№3, 2001,с.71, Москва, МГУ им. М.В. Ломоносова. (
http://rusnauka.narod.ru/lib/author/obuhov_yu_a/1/).
14. А. Чепик, Анализ
книги А. Эйнштейна, Л. Инфельда "Эволюция физики" , "Актуальные проблемы
статистической радиофизики", 2005, т.4, с.152-161,
http://redshift0.narod.ru/Rus/Stationary/Evolution_of_Physics_2.htm,
http://www.mptalam.org/a200513.html
, http://www.mptalam.org/200513.pdf
15.Л.И. Мандельштам "Лекции
по физическим основам теории
относительности. 1933-1934" Полное собрание
трудов Т. 5 (Под ред. М А Леонтовича) (М.-Л.:
Изд-во АН СССР, 1950) с. 90
16. Л.Д.Ландау, Е.М.Лифшиц.
Теория поля. (М., Наука, 1967.)
17. Логунов Л. А. Лекции по
теории относительности и гравитации:
Современный анализ проблемы. - М.: Наука. Гл.
ред. физ.-мат. лит., 1987.-272 с. ББК 22.313 Л 68 УДК
531.51
18. Г.Корн,Т.Корн. Справочник
математики. Наука, М.,1974.
19. R.Cahill, «A New Light-Speed Anisotropy
Experiment:
Absolute Motion and Gravitational Waves Detected», j. PROGRESS IN PHYSICS,
v.4, October 2006, p.73-92, [arXiv: physics/0610076v1],
http://www.mountainman.com.au/process_physics/HPS33.pdf,
http://arxiv.org/PS_cache/physics/pdf/0610/0610076v1.pdf,
(рус.яз -
http://redshift0.narod.ru/Rus/Stationary/References/Cahill_Absolute_2006_1.htm)
- - - - - - - -
Formula of the Velocity of Light in Medium in IFR of the LAST
Alexander M. Chepick
Nizhni Novgorod
e-mail: redshift0@narod.ru
Abstract
In this article the problem of a conclusion of the formula of speed of light in the medium with a known parameter of refraction is put and solved in the Theory of the Stationary Luminiferous Aether (LAST) on the basis of the classical law of refraction. It is clear that an orthogonality accepted in classical optics and in the SRT between a light's beam ( in the medium) and front of the light's wave is absent in LAST where the angle between the beam and front of a wave depends on speed of light in a given direction.
Key words: Absolute - LAST - inertial frame of reference - Eagle's transformation - Tangherlini's transformation - Transformation of Absolute - velocity of light in medium.
PACS: 01.55.+b, 01.65.+g, 98.80
- - - - - - - -
Вверх
Главная
страница
Eng
Последняя коррекция 07.02.2010 18:00:00