Preprint (03.05.2006)
Date: Wen, 03 May 2006 18:24:18 GMT
From: redshift0@narod.ru (Alexander Chepick)
Organization:
Newsgroups: sci.physics, alt.sci.physics.new-theories
Subject: Абсолютное пространство
Key words: Абсолют - выделенная система отсчета - эксперимент Майкельсона-Морли

Эксперимент Майкельсона-Морли не свидетельствует об отсутствии эфира

А.М. Чепик, Нижний Новгород,
e-mail: redshift0@narod.ru

Существует преобразование координат между ИСО в абсолютном пространстве, учитывающее результаты эксперимента Майкельсона-Морли (MMX).

1. Введение

На рубеже 19-20 веков Майкельсон и Морли[1] поставили ряд экспериментов (ММХ) по проверке возможного влияния эфирного ветра на скорость распространения электромагнитных волн. Эксперимент с достаточно высокой точностью показал, что такое влияние отсутствует. Лоренцу удалось объяснить этот результат при дополнительном предположении, что уравнения Максвелла, описывающие распространение электромагнитных волн, должны быть одинаковы во всех инерциальных системах отсчета (ИСО)[2]. Полученные им преобразования координат назвали Лоренцевскими. В начале 20 века Эйнштейн сумел вывести эти преобразования из более общей теоретической базы, названной им Специальной (частной) теорией относительности (СТО)[3]. При этом результат ММХ он назвал свидетельством отсутствия эфира.

Покажем, что MMX не требует отсутствия эфира.

2. Аналогия абсолютного пространства

Корабль, плывущий по спокойному озеру, является источником волн, однако от скорости корабля скорость этих волн не зависит. Тем более, скорость волн не может зависеть от скорости лодки-приемника, пересекающей их. Но относительная скорость волн зависит от скорости движения воды относительно приемника-наблюдателя (если только эталоны для измерения  скорости волн не созданы на этой лодке с помощью этих волн). Также от скорости лодки-наблюдателя зависит частота принимаемых волн, поэтому по распределению частот принимаемых волн наблюдатель на лодке может определить свою скорость относительно берега и неподвижной воды озера. (Что мы на Земле сумели выполнить для микроволнового фона.) Но если наблюдатель не покидает глубин океана и двигается в воде с достаточно малой скоростью (например, осьминог), то он не сможет определить анизотропию скорости звука в своей ИСО, и у него появятся основания для создания постулата о постоянстве скорости звука в воде в любой ИСО. Таким образом, независимость скорости света в вакууме от скорости источника или скорости приемника классически скорее является свидетельством наличия светоносной среды, чем отсутствия таковой.

3. Преобразования координат в Абсолютном пространстве

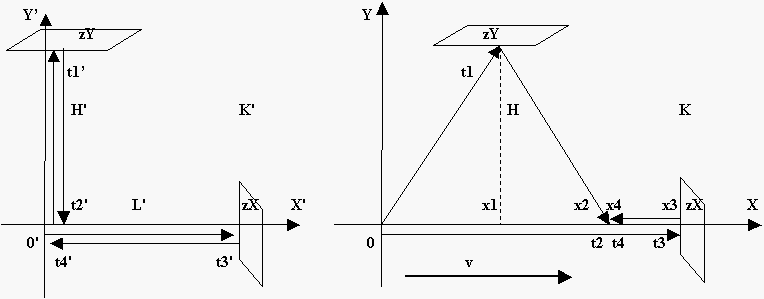
Следуя Максвеллу, мы будем предполагать существование эфира - изотропной среды, в которой распространяются электромагнитные колебания. Покажем, что существует решение для преобразований координат между ИСО K, неподвижной в эфире, и ИСО K', двигающейся в эфире с абсолютной скоростью v, не противоречащее результатам ММХ. Обозначим на Рис.1 координаты времени и места движения светового сигнала в ИСО K' (слева) и ИСО K (справа).

Pic.1.
В ИСО K' (слева) перпендикулярные лучи света, одновременно выходя из точки 0', возвращаются в нее же.  В ИСО K (справа) те же лучи света , одновременно выходя из точки 0, возвращаются в x₄ . Результаты эксперимента ММХ показывают, что времена возврата лучей (t₂' и t₄') в К' и (t₂ и t₄) в K совпадают с высокой точностью.

Пусть начало координат ИСО K' перемещается в ИСО K со скоростью v. Выпишем общий вид линейных преобразований координат из K в K' в случае совпадения в начальный момент t=0 соответствующих осей координат этих ИСО, причем ось X направлена в положительном направлении вектора v:

t'=a(v)x+b(v)t;  x'=d(v)x+e(v)t; y'=y; z'=z       (1)

Нахождение в явном виде функций a(v), b(v), d(v) и e(v) при некоторых условиях будем называть решением задачи поиска матрицы преобразования координат при этих условиях.

Как известно, Эйнштейн получил такое решение для двух ИСО (названное преобразованиями Лоренца[3]: a(v)=-γv/c², b(v)=d(v)=γ и e(v)=-γv,  где γ=[1-(v/c)²]^-½) при условии выполнения во всех ИСО двух постулатов:  скорость света c постоянная, законы физики инвариантные; и предположения о том, что матрица преобразования зависит только от одного параметра - относительной скорости ИСО. Тем самым он отказался от гипотезы о существовании эфира, как лишней, и гипотезы о выделенной системе отсчета, как противоречащей положениям теории.

Хотя при таких условиях Преобразование Лоренца является единственным решением системы (1), тем не менее это не означает, что при иных условиях не будет существовать другого решения той же системы. Но в рамках СТО рассматривать какое-нибудь предположение об эфире невозможно, так как СТО заведомо противоречит главное свойство неподвижного эфира - существование выделенной системы отсчета, в которой эфир неподвижен.

Поэтому для эфира необходимо построить другую теорию - в линейном пространстве.

ИСО, в которой эфир неподвижен, является выделенной (абсолютной) системой отсчета (АСО). В силу изотропии свойств эфира, скорость света в нем изотропная и ее величина равна некоторой константе c в АСО. Поэтому синхронизацию в АСО K можно проводить по методу Эйнштейна  или по методу медленного перемещения часов. Но синхронизацию в ИСО K' нельзя проводить по указанным методам, поскольку неизвестно, будет ли скорость света изотропной в K' и к какому пределу стремится показание перемещаемых часов при уменьшении их скорости движения. Поэтому синхронизацию в ИСО K' можно проводить  только по методу  синхронизации, при котором часы в каждой ИСО синхронизируются по одновременным событиям в АСО. Этот метод (MSN) не зависит от скорости света, для него совпадение моментов времени t двух разнесенных (x₁≠x₂) событий (t,x₁) и (t,x₂) в АСО соответствует совпадению соответствующих моментов времени t' этих событий (t',x'₁) и (t',x'₂) в ИСО (свойство одновременности любых двух событий в любых ИСО, если эти события одновременны хотя бы в одной ИСО). Подставим эти значения в (1): t'=b(v)t+a(v)x₁; t'=b(v)t+a(v)x₂; и получим  a(v)x₁=a(v)x₂ , то есть  a(v)=0. Из того, что нулевая точка K' двигается в K со скоростью v , следует, что   e(v)=-d(v)v. Таким образом, из (1) получаем систему уравнений:

t'=b(v)t;  x'=(x-vt)d(v); y'=y; z'=z       (2)

Итак, пусть АСО K - это абсолютная система отсчета с декартовой метрикой, в ней со скоростью v двигается ИСО K'.

Введем обозначения различных величин в K', задействованных в описании эксперимента ММХ (см. Рис.1.), нештрихованные координаты соответствующих событий в K вычисляются по формуле (2):
t₁' - момент отражения светового импульса от зеркала z_Y
t₃' - момент отражения светового импульса от зеркала z_X
t₂' - момент возврата перпендикулярного светового импульса в точку 0'
t₄' - момент возврата продольного светового импульса в точку 0'
H'  - длина перпендикулярного плеча до зеркала z_Y
L'  - длина продольного плеча до зеркала z_X
x₁' - X-координата места отражения светового импульса от зеркала z_Y
x₃' - X-координата места отражения светового импульса от зеркала z_X
x₂' - X-координата места возврата перпендикулярного светового импульса
x₄' - X-координата места возврата продольного светового импульса
с₀₁ - скорость перемещения светового импульса к зеркалу z_Y в K'
с₁₂ - скорость перемещения светового импульса от зеркала z_Y в K'
с₀₃ - скорость перемещения светового импульса к зеркалу z_X в K'
с₃₄ - модуль скорости перемещения светового импульса от зеркала z_X в K'
 H  - длина в ИСО K перпендикулярного плеча до зеркала z_Y
 L  - длина измеренного в ИСО K продольного плеча, двигающегося в ИСО K

Выпишем уравнения связи всех переменных :

В K' :
x₂' = x₄' = 0           (3) - лучи возвращаются в одну точку, 
H' = с₀₁t₁'            (4) - попадание луча в зеркало z_Y,
H' = с₁₂(t₂'-t₁')     (5) - возврат луча от зеркала z_Y,
L' = x₃' = с₀₃t₃'     (6) - попадание луча в зеркало z_X,
L' = с₃₄(t₄'-t₃')      (7) - возврат луча от зеркала z_X.
Особо отметим соотношение L' =H'   (8) которое следует из того, что наблюдатели в K' (в частности - мы) обязаны оперировать одним и тем же стандартом длины, независимо от направления этого эталона; а также  соотношения H=H'    (9) и H=L' =d(v)L    (10), получаемые из (2) и условия одновременности измерения в K длины L движущегося отрезка L'.

В K :
x₁ = vt₁                             (11) - путь, пройденный точкой 0' за время t₁,
(x₂-x₁) = v(t₂-t₁)                (12)  - путь, пройденный точкой 0' за время t₂-t₁,
H² + x₁² = с²t₁²                 (13) - длина пути луча к зеркалу z_Y,
H² + (x₂-x₁)²= с²(t₂-t₁)²    (14) - длина пути луча от зеркала z_Y,
vt₃+L = x₃ = сt₃                 (15) - путь, пройденный светом за время t₃,
vt₄ = x₄ =x₃ - с(t₄-t₃)          (16) - путь, пройденный светом за время t₄-t₃,

Из результата ММХ (картина интерференции не изменяется при повороте прибора [4,т.3,с.27]) следует, что к интерференционному экрану оба сигнала приходят в одной фазе, а поскольку от точки возврата лучей после отражения они проходят одинаковый путь в одних и тех же условиях, то из точки возврата лучей они также исходят однофазными в один и тот же момент, причем эта фаза от угла поворота прибора не зависит. А это возможно, только если в K' импульсы света возвращаются в точку 0' (практически) одновременно. Следовательно, из ММХ следует, что оба сигнала в K' возвращаются в начало отсчета практически одновременно, то есть: t₄' ≈ t₂'   (17).

Из (11-14) следует: 2x₁=x₂  (18), t₂ =2t₁   (19),   t₁ =γН/с  (20)
Из (15) следует: t₃ =x₃/с = L/(c-v)  (21)
Из (16,22) следует: t₄ =x₄/v = 2x₃/(c+v)= 2γ²L/с  (22)
Из построения ИСО K' следует : x₁' =x₂' =x₄' =0  (23) , так как это координаты начала отсчета  K'. 
Из (2,19,20) следует: t₁' =b(v)t₁ =b(v) γН/с   (24), t₂' =2b(v) γН/с    (25)
Из (2,21,22) следует: t₃' =b(v)t₃ =b(v)L/(c-v)  (26), t₄' =2b(v)γ²L/с   (27)
Из (17,25,27) следует: Н ≈ γL   (28)

Считая соотношение t₄'≈ t₂'  экспериментальным проявлением точного равенства t₄' = t₂'  (29), получаем из (10,28) величину функции  d(v): d(v)=γ  (30).

Рассматривая прибор (интерферометр Майкельсона) в качестве световых часов, совершающих один полный цикл действий от начала движения импульса света до возврата его в ту же точку, и исходя из единицы времени "один полный цикл прибора" в любой ИСО, получаем при анализе движения импульса света вдоль плеча H', что с точки зрения ИСО K один полный цикл t₂' часов в ИСО K' выполнится за время  γt₂ по такому же неподвижному в K прибору, в силу движения в K светового импульса с одинаковой скоростью по гипотенузе и по катету соответственно (см. Рис.1). То есть, время в единицах "полный цикл" в K' идет медленнее в  γ раз, чем в единицах "полный цикл" в K. Но этот частный случай сравнения времени в разных ИСО должен выражаться общей формулой (2). Откуда с учетом формулы t'=b(v)t получаем  b(v)=1/γ   (31).

Рассчитаем скорости движения импульсов света в ИСО K' :
Из (4,5,8,24,25,31) следует: с₀₁ =с₁₂ =H'/t₁'=c/(b(v)γ)=c        (32)
Из (6,10,27,30,31) следует: с₀₃=L'/t₃' =γ(c-v)/ b(v)=c/(1+v/c)   (33)
Из (7,10,26,27,30,31) следует: с₃₄= L'/(t₄'-t₃')= c/(1-v/c)          (34)

Следовательно, в K' получаем анизотропную скорость света. Обозначив в K' a' - угол отклонения скорости света от направления скорости v, получим общую формулу скорости света в K' :

с'(v,a')=c/(1+(v/c)cos a')      (35)

4. Выводы

1. Эксперимент Майкельсона - Морли не отрицает эфир и выделенную систему отсчета.

2. Существует преобразование координат в абсолютном пространстве из АСО в ИСО, не противоречащее результатам эксперимента Майкельсона - Морли:   t'=t/γ; x'=γ (x-Vt); y'=y; z'=z.

Литература:
[1] Miller D.C Significance of the ether-drift experiments of 1925 at Mount Wilson. Sd. 1926. Vol. 68, N 1635.
[2] Лоренц Г.А. Теория электронов и ее применение для явлений света. (М.: Гос. издат. техн.-теор. лит., 1953,с. 280-307)
[3] Эйнштейн А. К электродинамике движущихся тел. Собр. трудов, т.1. М., Наука, 1965.
[4] Физическая энциклопедия, (М., Советская энциклопедия,1990, т.3,с.27)

- - - - - - - -

Michelson-Morley Experiment does not testify to Absence of an Ether
Alexander M. Chepick, Nizhni Novgorod, e-mail: redshift0@narod.ru

 

Главная страница                               Eng

Последняя коррекция 08.03.2008 16:02:15